Binary Tree adalah: Ciri-ciri, Fungsi, Jenis Struktur Data

Binary tree adalah salah satu struktur data yang sangat penting dalam dunia ilmu komputer. Tapi apa sebenarnya binary tree itu? Berikut ulasan tentang binary tree, ciri-cirinya, fungsinya, serta bagaimana cara mengaksesnya.

Apa itu Binary Tree?

Secara sederhana, binary tree (pohon biner) adalah struktur hierarkis yang terdiri dari node-node yang saling terhubung. Setiap node dalam pohon biner memiliki dua anak, yaitu anak kiri dan anak kanan. 

Masing-masing anak tersebut juga bisa memiliki dua anak lagi, dan begitu seterusnya. Ini membentuk suatu struktur yang bercabang, mirip dengan cabang-cabang pohon.

Keuntungan utama dari struktur ini adalah kemampuannya untuk mengorganisir data dan melakukan berbagai operasi dengan cara yang efisien. 

Sebagai contoh, pencarian data dalam pohon biner dapat dilakukan lebih cepat karena sifat hierarkinya, yang membantu mempersempit ruang pencarian. 

Jadi, dibandingkan dengan struktur data lain yang lebih sederhana, seperti array atau linked list, pohon biner menawarkan keunggulan dalam hal efisiensi.

Inti dari binary tree adalah sama, yakni mengorganisasi data dalam bentuk struktur hierarkis yang memudahkan berbagai operasi.

Ciri-ciri Mendasar Binary Tree

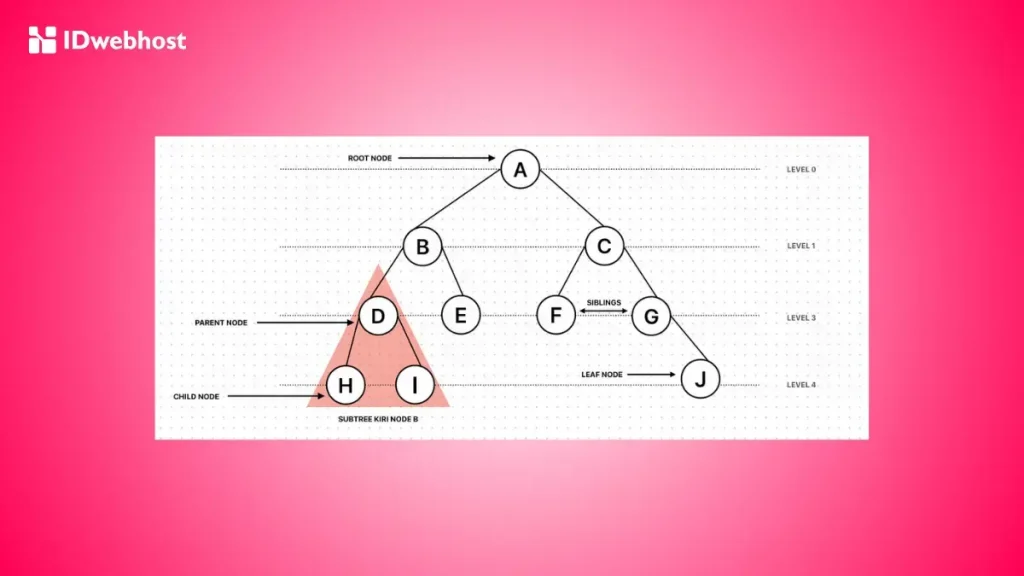
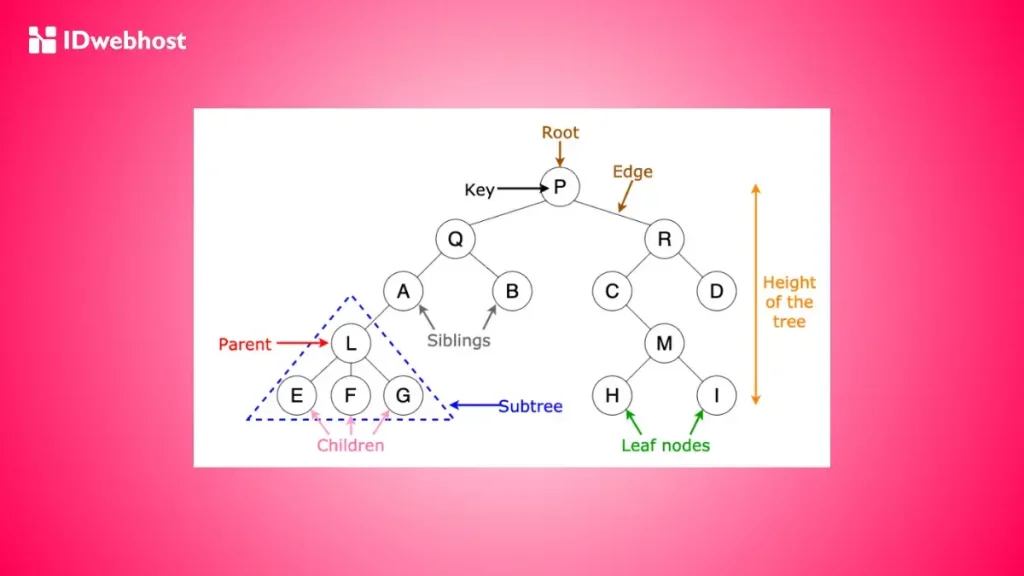
Untuk memahami lebih dalam, ada beberapa ciri-ciri mendasar dari pohon biner yang perlu kamu ketahui:

• Node: Setiap elemen dalam binary tree disebut node. Node ini menyimpan data dan memiliki dua bagian utama, yaitu data dan pointer (referensi atau alamat yang menunjuk ke anak kiri dan kanan, jika ada).
• Root: Root atau akar adalah node pertama dalam pohon yang menjadi titik awal untuk mencapai semua node lainnya.
• Anak Kiri dan Anak Kanan: Setiap node dalam pohon biner bisa memiliki dua anak, yaitu anak kiri dan anak kanan. Namun, ada kemungkinan suatu node hanya memiliki satu anak atau bahkan tidak memiliki anak sama sekali (leaf node).
• Tingkat Kedalaman dan Tinggi Pohon: Depth (kedalaman) dari sebuah node adalah panjang jalur dari root ke node tersebut. Sedangkan height (tinggi) pohon adalah panjang jalur terpanjang dari root ke salah satu leaf node.
• Leaf Node: Leaf node adalah node yang tidak memiliki anak, dan biasanya menjadi titik akhir dalam jalur dari root.
• Subtree: Setiap node dalam pohon biner beserta anak-anaknya membentuk sebuah subtree.

Fungsi Binary Tree

Secara umum, ada beberapa fungsi dasar dari pohon biner yang sering diterapkan dalam berbagai aplikasi komputer:

• Penyimpanan Data: Pohon biner digunakan untuk menyimpan data secara terstruktur, yang memungkinkan pencarian dan manipulasi data lebih cepat dibandingkan dengan struktur data linear seperti array atau linked list.
• Pencarian Data: Pada binary search tree (BST), pencarian dilakukan dengan cara membandingkan nilai node dan menelusuri anak kiri atau kanan. Proses ini memungkinkan pencarian yang lebih efisien, dengan waktu kompleksitas yang lebih rendah dibandingkan pencarian linear.
• Pengurutan Data: Salah satu kegunaan pohon biner adalah untuk mengurutkan data. Setiap elemen yang ditambahkan ke dalamnya akan terurut secara otomatis ketika pohon ditelusuri.
• Hierarki dan Relasi: Pohon biner sering digunakan untuk menggambarkan struktur hierarkis, misalnya dalam sistem manajemen organisasi atau hubungan antar posisi dalam sebuah organisasi.
• Optimisasi: Jenis khusus dari pohon biner, seperti AVL tree atau Red-Black tree, dapat digunakan untuk menjaga keseimbangan pohon, sehingga operasi seperti pencarian dan pengurutan tetap optimal.

Jenis-Jenis Binary Tree

Ada beberapa jenis pohon biner yang sering digunakan dalam berbagai aplikasi komputer. Berikut di antaranya:

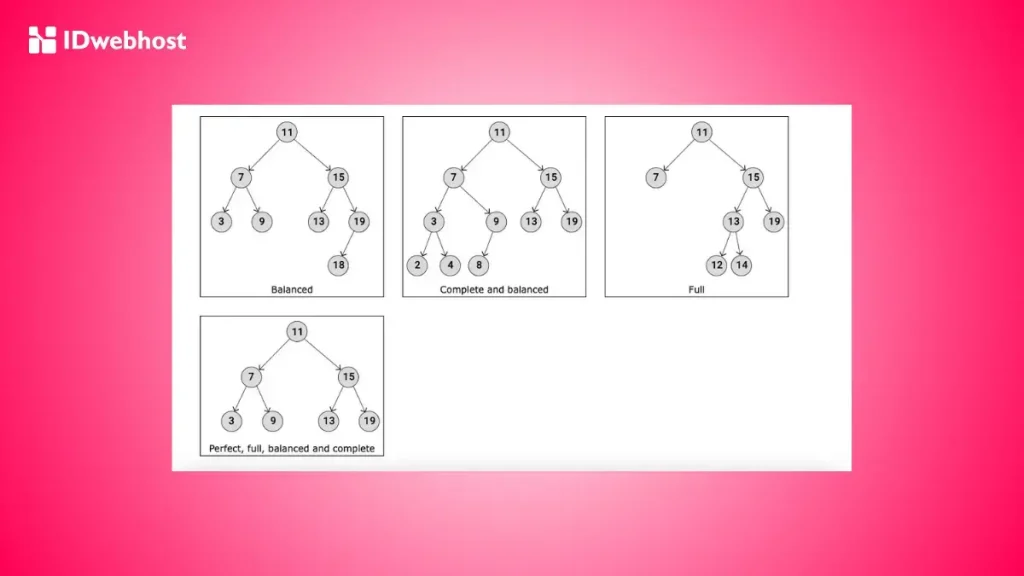
1. Pohon Biner Penuh (Full Binary Tree)

Pohon biner penuh adalah pohon yang setiap node internalnya memiliki tepat dua anak, kecuali mungkin daun yang ada di level paling bawah. Semua node internal memiliki dua anak, dan tidak ada node internal yang hanya memiliki satu anak.

2. Pohon Biner Lengkap (Complete Binary Tree)

Pohon biner lengkap adalah pohon di mana setiap levelnya terisi sepenuhnya, kecuali pada level terakhir yang diisi dari kiri ke kanan. Meskipun level terakhir tidak sepenuhnya penuh, pohon ini tetap dianggap lengkap karena urutan pengisian dimulai dari kiri.

Contoh pohon biner lengkap:

     1
   /   \
  2     3
 / \
4   5

3. Pohon Biner Sempurna (Perfect Binary Tree)

Jenis ini memiliki pohon yang setiap node internalnya punya dua anak, dan semua daun berada pada level yang sama. Dengan kata lain, jika pohon biner penuh juga sempurna, maka pohon biner sempurna adalah pohon yang lebih terstruktur lagi.

Contoh pohon biner sempurna:

     1
   /   \
  2     3
 / \   / \
4   5 6   7

Pada contoh ini, semua node memiliki dua anak, dan semua daun berada di level yang sama.

4. Pohon Biner Seimbang (Balanced Binary Tree)

Pohon biner seimbang adalah pohon di mana selisih tinggi antara subpohon kiri dan subpohon kanan dari setiap node tidak lebih dari satu. Keseimbangan ini penting untuk menjaga kecepatan operasi pencarian dan penyisipan.

Contoh pohon biner seimbang:

     1
   /   \
  2     3
 /     /
4     5

Pohon ini masih seimbang karena selisih kedalaman antara subpohon kiri dan kanan tidak lebih dari satu.

5. Pohon Biner Degenerasi (Degenerate Binary Tree)

Pohon biner degenerasi adalah pohon yang setiap node hanya memiliki satu anak, sehingga strukturnya menyerupai linked list. Meskipun ini masih bisa dianggap sebagai pohon biner, efisiensinya dalam pencarian menjadi lebih rendah.

Contoh pohon biner degenerasi:

1
 \
  2
   \
    3
     \
      4

Pohon ini sebenarnya berfungsi seperti daftar tertaut, di mana setiap node hanya memiliki satu anak.

Operasi pada Pohon Biner

Operasi dasar yang sering dilakukan pada pohon biner antara lain:

1. Penyisipan (Insertion)

Proses menambahkan node baru ke dalam pohon biner. Biasanya, pada pohon biner lengkap, node baru akan ditambahkan pada posisi kosong pertama yang ditemukan dari kiri ke kanan untuk menjaga struktur pohon tetap teratur.

Contoh penyisipan: Misalkan kita ingin menambahkan angka 6 ke dalam pohon biner berikut:

    1
   /   \
  2     3
 / \
4   5

Setelah angka 6 disisipkan, pohon akan terlihat seperti ini:

    1
   /   \
  2     3
 / \   /
4   5 6

Node baru (6) akan ditambahkan di posisi kosong yang pertama ditemukan dari kiri ke kanan.

2. Pencarian (Search)

Pencarian dilakukan untuk menemukan nilai tertentu dalam pohon biner. Pencarian dapat dilakukan dengan menelusuri pohon secara rekursif atau menggunakan metode traversal tertentu.

Contoh: Jika kita ingin mencari angka 5 dalam pohon biner berikut:

    1
   /   \
  2     3
 / \
4   5

Pencarian akan dimulai dari node akar (1), lalu dilanjutkan menuju anak kiri atau kanan, hingga angka 5 ditemukan.

3. Penghapusan (Deletion)

Penghapusan adalah proses menghapus sebuah node dari pohon biner. Biasanya, node yang akan dihapus digantikan dengan node yang berada di posisi terdalam (paling bawah dan paling kanan) dalam pohon, kemudian struktur pohon disesuaikan.

4. Traversal

Traversal adalah proses untuk mengunjungi setiap node dalam pohon dengan urutan tertentu. Beberapa metode traversal yang umum digunakan antara lain:

• In-order Traversal: Mengunjungi anak kiri terlebih dahulu, kemudian akar, dan terakhir anak kanan.
• Pre-order Traversal: Dimulai dengan mengunjungi akar, lalu anak kiri, dan kemudian anak kanan.
• Post-order Traversal: Mengunjungi anak kiri, kemudian anak kanan, dan terakhir akar.
• Level-order Traversal: Mengunjungi node berdasarkan level, dimulai dari root.

Contoh traversal untuk pohon biner berikut:

    1
   /   \
  2     3
 / \
4   5

Hasil traversalnya adalah:

• In-order: 4, 2, 5, 1, 3
• Pre-order: 1, 2, 4, 5, 3
• Post-order: 4, 5, 2, 3, 1
• Level-order: 1, 2, 3, 4, 5

Setiap jenis traversal memiliki kegunaannya sendiri, tergantung pada tujuan atau masalah yang ingin diselesaikan.

Kesimpulan

Binary tree adalah struktur data hierarkis yang terdiri dari node-node yang saling terhubung, di mana setiap node dapat memiliki dua anak (kiri dan kanan). Struktur ini memudahkan dalam penyimpanan, pencarian, pengurutan, dan pengelolaan data.

Di sisi lain, jika kamu sedang mencari layanan yang dapat mendukung implementasi struktur data ini, IDwebhost menawarkan berbagai pilihan hosting yang optimal, serta mendukung aplikasi yang membutuhkan pengolahan data besar dengan efisien.